STATISTIK DESKRIPTIF
A. PENGERTIAN STATISTIK
Statistika adalah cabang ilmu yang mempelajari tentang bagaimana mengumpulkan, menganalisis dan menginterpretasikan data. Atau dengan kata lain, statistika menjadi semacam alat dalam melakukan suatu riset empiris.Dalam
menganalisis data, para ilmuwan menggambarkan persepsinya tentang suatu
fenomena. Deskripsi yang sudah stabil tentang suatu fenomena seringkali
mampu menjelaskan suatu teori.
Secara umum kedudukan statistika memiliki beberapa manfaat,
antara lain:
a. Menyajikan data secara ringkas dan jelas, sehingga lebih mudah
dimengerti oleh para pengguna.
b. Menunjukkan trend atau tendensi perkembangan suatu masalah.
c. Melakukan penarikan kesimpulan secara ilmiah.
B. PENGERTIAN STATISTIK DESKRIPTIF
Statistik Deskriptif adalah statistik yang berfungsi untuk mendiskripsikan atau memberi gambaran terhadap obyek yang di teliti melalui data sampel atau populasi sebagaimana adanya, tanpa melakukan analisis dan membuat kesimpulan yg berlaku untuk umum.
Pada statistik deskriptif ini akan di kemukakan cara - cara penyajian data dengan tabel biasa maupun distribusi frekuensi : grafik garis maupun maupun batang; diagram lingkaran; pictogram; penjelasan kelompok melalui modus, median, mean, dan variasi kelompok melalui rentang dan simpangan baku.
C. PENGUKURAN GEJALA PUSAT ( CENTRAL TENDENCY )
Setiap penelitian selalu berkenaan dengan sekelompok dengan sekelompok data. yang di maksud kelompok disini adalah, salah satu orang mempunyai sekelompok data, atau sekelompok orang mempunyai satu macam data misalnya, sekelompok murid di kelas dengan satu nilai mata kuliah. gabungan dengan kedua misalnya sekelompok, mahasiswa di kelas dengan berbagai nilai mata kuliah.
teknik penjelasan kelompok bisa jelaskan dengan menggunakan teknik statistik yang di sebut: Modus, Median, dan Mean
Modus merupakan teknik penjelasan teknik penjelasan kelompok yang di dasarkan atas nilai yang sedang populer ( yang sedang menjadi mode ) atau nilai yang sering muncul dalam kelompok dalam kelompok tersebut.
Rumus:
Rumus mencari modus :
Keterangan :
L = batas bawah nyata (tepi bawah) dari kelas modus
d1 = selisih antara frekuensi dari kelas yang
mengandung modus dan frekuensi dari kelas yang mendahuluinya (sebelumnya).
d2 = selisih antara frekuensi dari kelas yang
mengandung modus dan frekuensi dari kelas berikutnya
i = interval kelas/panjang kelas.
data : 4 7 2 3 2 7 7 9 4 modus dari data tersebut adalah : 7
contoh soal modus data kelompok :
Berapa modus dari data kelompok berikut dan bagaimana cara menghitung modusnya?
Interval Kelas (c) = 5
Batas Bawah Kelas modus = 35,5 fo = 150 f1 = 70 f2 = 90 | |||||||||||||||||
| jadi modusnya = 35,5 + 5 (80/(80+60)) = 35,5 + 5 (80/140) = 35,5 + 2,86 = 38,36 | |||||||||||||||||
Median adalah salah satu teknik penjelasan kelompok yang didasarkan atas nilai tengah dari kelompok data yang telah di susun urutannya dari yang terkecil sampai yang terbesar, atau sebaliknya dari yang terbesar sampai terkecil.
Rumus mencari median :
Keterangan :
Lo = tepi bawah dari kelas limit yang
mengandung median,
Me
= nilai median,
n =
banyaknya data,
Fk =
frekuensi kumulatif sebelum kelas yang memuat median,
f0 =
frekuensi kelas yang memuat median,
c = panjang intreval kelas
data : 4 7 2 3 2 7 7 9 4
data terurut : 2 2 3 4 4 7 7 7 9

contoh soal median data kelompok :
| Kelas | Frekuensi | F Kumulatif |
| 15-19 |
5 | 5 |
| 20-24 |
7 | 12 |
| 25-29 |
10 | 22 |
| 30-34 |
15 | 37 |
| 35-39 |
13 | 50 |
| 40-44 |
8 | 58 |
| 45-49 |
3 | 60 |
Dari tabel di atas dapat diketahui bahwa median adalah suku antaran suku ke 29 dan suku ke 30 dan kelas letak median ada di kelas 30-34. Jadi
Median = 29,5 +[(30-37)/15] 5 = 27,16
Jadi median dari data kelompok di atas adalah 27,16
3. Mean
Mean merupakan teknik penjelasan kelompok yang di dasarkan atas nilai rata - rata dari kelompok tersebut. Rata - rata ( mean ) ini di dapat dengan menjumlahkan data seluruh individu dalam kelompok itu, kemudian di bagi dengan jumlah individu yang ada pada kelompok tersebut.
Rumus mean data tunggal :
contoh soal mean data tunggal :
data : 4 7 2 3 2 7 7 9 4

Rumus mean data kelompok :
Keterangan :
Keterangan :
fi : frekuensi untuk nilai untuk Xi yang bersesuaian.
X0 : tanda kelas dengan nilai sandi ci = 0.
Tanda kelas yang lebih besar dari X0 berturut-turut
mempunyai harga +1,
contoh soal mean data kelompok :
Diketahui data tinggi badan sekelompok siswa sebagai berikut.
Tinggi Badan
|
Frekuensi
|
131 – 140
141 – 150
151 – 160
161 – 170
171 – 180
181 – 190
|
2
5
13
12
9
4
|
Hitunglah rerata (mean) data tersebut.
Rata-rata
= (2(135,5) + 5(145,5) + 13(155,5) + 12(165,5) +9(175,5) + 4(185,5)) / (2 + 5 + 13 + 12 + 9 + 4)
= (271 + 727,5 + 2021,5 + 1986 + 1579,5 + 724 ) / (2 + 5 + 13 + 12 + 9 + 4)
= 7327,5 / 45
= 162,83
D. PENYAJIAN DATA DALAM BENTUK DIAGRAM
Sering kali data yang disajikan dalam bentuk tabel sulit untuk dipahami.
Lain halnya jika data tersebut disajikan dalam bentuk diagram maka Anda
akan dapat lebih cepat memahami data itu. Diagram adalah gambar yang
menyajikan data secara visual yang biasanya berasal dari tabel yang
telah dibuat. Meskipun demikian, diagram masih memiliki kelemahan, yaitu
pada umumnya diagram tidak dapat memberikan gambaran yang lebih detail.
a. Diagram Batang
Diagram batang biasanya digunakan untuk menggambarkan data diskrit (data
cacahan). Diagram batang adalah bentuk penyajian data statistik dalam
bentuk batang yang dicatat dalam interval tertentu pada bidang
cartesius.
Ada dua jenis diagram batang, yaitu
- diagram batang vertikal, dan
- diagram batang horizontal.
a. Diagram batang vertikal dari data tersebut, tampak pada gambar berikut.
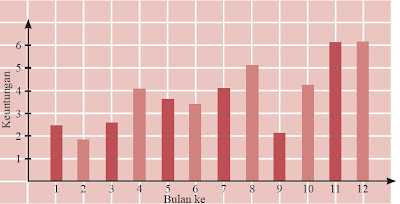
b. Diagram Garis
Pernahkah Anda melihat grafik nilai tukar dolar terhadap rupiah atau
pergerakan saham di TV? Grafik yang seperti itu disebut diagram garis.
Diagram garis biasanya digunakan untuk menggambarkan data tentang m
keadaan yang berkesinambungan (sekumpulan data kontinu). Misalnya,
jumlah penduduk setiap tahun, perkembangan berat badan bayi setiap
bulan, dan suhu badan pasien setiap jam.
Seperti halnya diagram batang, diagram garis pun memerlukan sistem sumbu
datar (horizontal) dan sumbu tegak (vertikal) yang saling berpotongan
tegak lurus. Sumbu mendatar biasanya menyatakan jenis data, misalnya
waktu dan berat. Adapun sumbu tegaknya menyatakan frekuensi data.
Langkah-langkah yang dilakukan untuk membuat diagram garis adalah
sebagai berikut.
- Buatlah suatu koordinat (berbentuk bilangan) dengan sumbu mendatar menunjukkan waktu dan sumbu tegak menunjukkan data pengamatan.
- Gambarlah titik koordinat yang menunjukkan data pengamatan pada waktu t.
- Secara berurutan sesuai dengan waktu, hubungkan titiktitik koordinat tersebut dengan garis lurus.

c. Diagram Lingkaran
Untuk mengetahui perbandingan suatu data terhadap keseluruhan, suatu
data lebih tepat disajikan dalam bentuk diagram lingkaran. Diagram
lingkaran adalah bentuk penyajian data statistika dalam bentuk lingkaran
yang dibagi menjadi beberapa juring lingkaran.
Langkah-langkah untuk membuat diagram lingkaran adalah sebagai berikut.
- Buatlah sebuah lingkaran pada kertas.
- Bagilah lingkaran tersebut menjadi beberapa juring lingkaran untuk menggambarkan kategori yang datanya
- telah diubah ke dalam derajat.


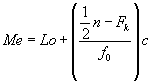


Good ;)
BalasHapusmksh kak :)
BalasHapusCasino-Casino.com MapYRO
BalasHapusCasino-Casino.com is a 안동 출장마사지 website where you can 순천 출장마사지 find information about 문경 출장안마 Casino-Casino.com. Check the location, timings, 안양 출장안마 and 청주 출장샵 contact information.